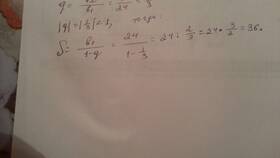Сумма бесконечной геометрической прогрессии существует при определенных условиях и может быть вычислена по специальной формуле. Этот математический инструмент применяется в различных областях - от финансовых расчетов до физических моделей.
Содержание
Условия существования суммы
Критерий сходимости
- Знаменатель прогрессии |q| < 1
- При |q| ≥ 1 сумма расходится
- Прогрессия должна быть бесконечной
Формула суммы бесконечной геометрической прогрессии
| Обозначение | Описание |
| S | Сумма прогрессии |
| b₁ | Первый член прогрессии |
| q | Знаменатель прогрессии (|q| < 1) |
Основная формула
S = b₁ / (1 - q)
Пошаговый алгоритм вычисления
- Определите первый член прогрессии (b₁)
- Вычислите знаменатель прогрессии (q)
- Проверьте условие |q| < 1
- Подставьте значения в формулу S = b₁ / (1 - q)
- Выполните вычисления
Пример расчета
- Дано: 8 + 4 + 2 + 1 + ...
- b₁ = 8
- q = 1/2 (так как 4/8 = 0.5)
- S = 8 / (1 - 0.5) = 16
Практическое применение
| Область | Пример использования |
| Экономика | Расчет мультипликативного эффекта инвестиций |
| Физика | Определение общего сопротивления цепочки |
| Биология | Моделирование популяций с ограниченным ростом |
Особые случаи
- При q = 0 сумма равна первому члену
- При q → 1 сумма стремится к бесконечности
- Для знакопеременных прогрессий (q < 0) формула сохраняется
Дополнительные замечания
Для проверки правильности вычислений можно рассчитать частичные суммы прогрессии и проследить их приближение к найденному значению. В случае сомнений в сходимости ряда рекомендуется использовать признаки сходимости или консультироваться с математическими справочниками.